Proving in propositional logic, Conditional and Indirect proofs

In my second-to-last article, we continued our exploration of propositional logic, where we studied the elements and rules of propositional logic. These are things like the capital words P, Q, R, symbols like v, ^, -, >, and rules like modus ponens and Demorgans. (“The Truth: Propositional Logic”)

Then, we studied the basic sketch mechanism of proofs in propositional logic: proof tables. (“Proving in propositional logic”). Today, we are looking at the second part of proofs in propositional logic, Conditional and Indirect proofs.

The first type of proof, Conditional proof, is fairly basic. If we wish to prove that some statement P implies some statement Q, that is if we wish to prove that P > Q, we can assume that P is true. By doing so, if afterwards we solely use this assumption and the premises we’ve previously had, we will aim to conclude Q. So, this would mean that when P is assumed, Q can be concluded. That is exactly what implication means: P > Q means that when P is true, Q must follow.

Here is an example:

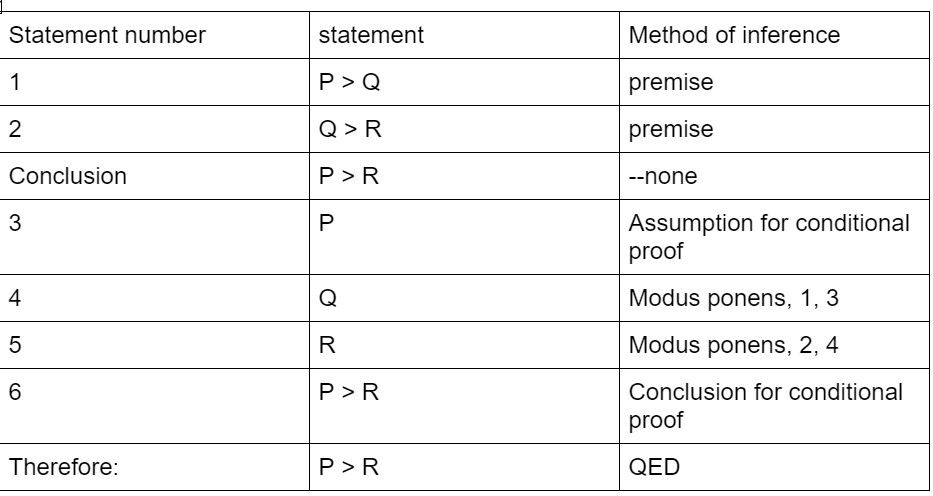
The next proof type, is the method of indirect proof: If we are very sure that some statement P must be true, we can create the theoretical scenario that P is false. If we actually are right that P must be true, we can show that when P is false, something wrong will happen, like a contradiction. That is, if given -P, we can conclude that Q^-Q for some statement Q.

This is the definition of contradiction: Q^-Q is obviously meaningless, how can something both be true and false? We can even show the problem of having such a statement Q exist: we can simplify this statement as Q, and also as -Q. Then, we can perform addition to get QvF, for any statement F. Then, through disjunctive syllogism, we can conclude F. This leaves us with the ability to make anything be true! Any F, must be true given that Q^-Q is true. That breaks our logic, makes it meaningless, as it becomes a system with no distinction between true and false.

If this whole Indirect proof thing seems confusing, don’t worry. It will become clearer as we study it with an example:

Next month, I will not be making another propositional logic article, since the past 3 have already covered all of the content of it! If you’ve understood the last 3 articles, you’ve learned propositional logic! What we will study next month, is what the past 4 articles have been leading up to First-order logic. It is the basis of Set Theory, an important theory that is served as the foundation of mathematics.

Gabriel Tonini, 28/01/22.