Proving in propositional logic

In my last article, I covered the alphabet (formally the ‘syntax’) of propositional logic, and also the rules that of propositional logic. If you don’t recall, these are all of the elements of the propositional syntax:

And the rules of propositional logic are:

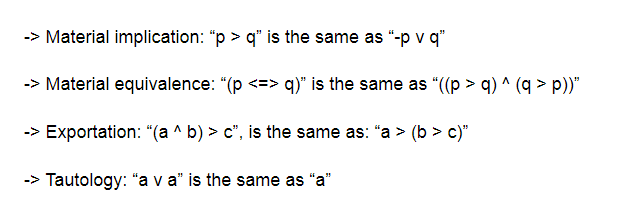
So how can we actually prove things? You may have done this before in math class, but if not, here is the basic process:

We have a list of premises, assumptions. These assumptions are the things we take as facts. If I say that it is raining today, that is my assumption to prove whatever I want to. Another assumption we might have is that “whenever it’s raining, I will wear a coat.”. Then, these two statements are our assumptions. The other component of proof is the thing we want to prove. If we want to prove that I will wear a coat today (since it is raining), we must articulate a proof for that. The part we want to prove is called the conclusion of the proof.

Then, we would say that the premises are:

-It is raining today

-If it rains, I am wearing a coat

And the conclusion is:

-I am wearing a coat

To actually prove this in the language of propositional logic, we must convert these statements into the language. The first statement is easy, we can just make it a capital word, R, which is true when it’s raining

The second statement could be broken down into an implication: R > C, where C is true when I am wearing a coat. The conclusion that we wish to prove, is C itself. We want to show that I am going to wear a coat today. The whole argument then looks like this: P1: R, P2: R > C, Conclusion: C. This way of saying “P” and then a number, is just the common way to list the premises at play. This proof can actually be done quite easily. All that must be done is modus ponens. This can be applied to premises 1 and 2, and will yield the conclusion, C.

The formal way this is written, is using a proof table:

And as the cherry on top, mathematicians and logicians like to write QED, which stands for Latin ’quod erat demonstrandum’, meaning "which was to be demonstrated". Literally it states "what was to be shown". Another proof that I will show you, is one involving De morgans:

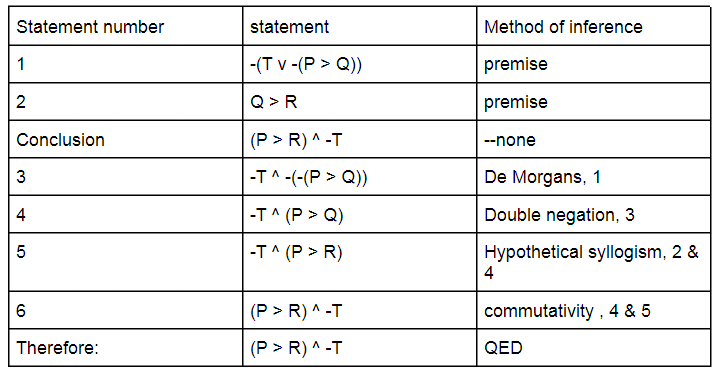
Now, next time, I will show other methods of proof that involve propositional logic. Stay tuned!