Game Theory: Mathematical Model of Strategic Behaviour Give Us Insight About Life, Relations, War

Prologue

Today, I aim to cover key game theory principles, while using real life “games” to exemplify and give the reader a better digestion of the concepts.

We will furthermore make a case study on the recent Russian-Ukranian war, through the lens of strategically-minded game theorists. I understand sorrowfully that the topic can be sensitive to some, and wish not to give or conclude any opinions on the situation, but rather look at it from a resource-based perspective in order to study the political//military distribution of power.

We will lastly pay homage to the game theorists that have made the concepts studied here, by covering some historical background of game theory.

I recommend the reader to read this article in whichever way suits best, whether that be in a single seating or in a series of short reads. It is in no one’s capability to easily digest the main ideas discussed here without a required level of attention and patience, meaning it is ok to find some of the concepts at hand hard to grasp at first.

Game Theory Foundations

In game theory, a game is more complicated than a winning-losing leisure, but rather, a game is formally defined as a strategically interdependent situation. What this means is that in a game, players (a.k.a. participants) will have different strategies (a.k.a. actions) that they can make. For example, in the famous prisoner dillemma, the players can choose between two actions/strategies, either to snitch on the other prisoner, or to keep quiet and not say anything.

Now here’s where the “interdependence” comes in. the actions of either player are dependent on the actions of the other players: if one player snitches, the other gets punished, and so on. The point, is that whatever actions a player makes, that action is going to effect in some way the other players’s outcome.

This “outcome”, is formally known as the payoff. The payoff, is the amount of reward//punishment gained from a certain event. For example, the payoff will be very bad if the other prisoner snitches on you, while it won’t be as bad if the player does not. So interdependence is formally defined as when the strategy of a player affects the payoffs of others.

Now how can we visualise a game, without using words? The way used in game theory is a bit aligned with the way a probabilist would go about the problem.

The way that is done is through a table of possible outcomes, which is formally called the payoff matrix (a definition we will get to later on):

Player 1’s first strategy Player 1’s second strategy Player 2’s first strategy Player 2’s second strategy

This table simplifies all possible events that can happen. Say that in a game, player 1 follows a possible strategy, their first, and the second player follows their second strategy, this situation could be labelled as the cube on the bottom left of the table:

Player 1’s first strategy Player 1’s second strategy Player 2’s first strategy Player 2’s second strategy The outcome when player 1 chooses their first strategy and player 2 chooses their second

Bringing this back to earth, take a look at the payoff matrix for the prisoner’s dilemma:

Prisoner 1 snitches Prisoner 1 keeps quiet Prisoner 2 snitches -10, -10 -12, 0 Prisoner 2 keeps quiet 0, -12 -1, -1

The numbers listed on the previously empty event boxes, represent the payoffs of each prisoner given that the event happens. Negative payoffs can be seen as punishments, as they imply negative rewards, while positive payoffs can be seen as rewards. Then, what this table shows, is that when both prisoners snitch on each other, they both receive 10 months in jail (say that the payoff is measured in months), but if one prisoner snitches and the other keeps quiet, the snitch won’t get any month in jail, while the other will get 12, and if both prisoners don’t snitch, they each get to spend only a month in jail.

Now, the purpose of the games we will be analysing today, is to look at a player’s outcomes, and try to maximise it, using rationality. In this case, it can be easily noticed that the best outcome for both prisoners is to keep quiet, as such an outcome will minimise the overall time spent in jail.

But, contrary to this notion, researchers have gone to find (in several studies with real participants), that keeping quiet is not what players are statistically likely to do, just like in Split or Steal, only around half the time, players choose to split.

The problem with keeping quiet, is the age-old question of trust. If one chooses to keep quiet, they are vulnerable to getting snitched at and going to jail for a long time. Since players do not wish to take such a risk, they are lead to both snitch.

While bad for the prisoners, this situation/game, is good for law enforcers, as they have cornered suspects into a situation where they are logically prown to snitch, meaning more wrong-doers will confess their crimes.

What game theorists are really interested in, is this logic of trust, risk, and certainty. The solution to this problem, on whether to trust one or not, is the Nash equilibrium. The nash equilibrium is the basis of all game theory, so it is important we recapitulate what we’ve learned so far into the assumptions//rules of game theory:

• Every game has 2 or more players

• Every event (unique combination of actions) has payoffs for all players

• All players are assumed to be completely rational given game theoretic standards

• Every player is self-interested and does not care about other player’s payoffs

With exception to the last rule (which sometimes may not be in cooperative games), game theory assumes these as facts to any game.

To understand Nash equilibrium, we must first learn dominant strategies. In the game of the prisoners, on the payoff matrix, we see a pattern arise to prisoner 1’s actions:

Prisoner 1 snitches Prisoner 1 keeps quiet Prisoner 2 snitches -10, -10 -12, 0 Prisoner 2 keeps quiet 0, -12 -1, -1

Independently of what prisoner 2 chooses, player 1 is always better off confessing. This is because if prisoner 2 snitches, for prisoner 1 to keep quiet will earn them 2 months in jail, meaning if prisoner 2 snitches, prisoner 1 is better off snitching as well. And if prisoner 2 keeps quiet, 0 months in jail is better than 1 month in jail.

What this implies, is that independently of what prisoner 2 does, prisoner must rationally snitch. This is called strict dominance. What has happened is that the snitching strategy for prisoner 1 has strictly dominated the keeping quiet strategy.

This effect of strict dominance allows all players to eliminate prisoner 1 from keeping quiet from the list of options:

Prisoner 1 snitches Prisoner 2 snitches -10, -10 Prisoner 2 keeps quiet 0, -12

Describes all the rational events that remain. But wait, if prisoner 2 keeps quiet, they will innevitably earn 2 more months in jail than if they snitch, meaning it is also to prisoner 2’s logical advantage to snitch as well.

What this leaves us, is that the only logical ending to the game is that both players snitch:

Prisoner 1 snitches Prisoner 2 snitches -10, -10

This revelation, has brought us to the Nash equilibrium of this game, the snitch-snitch scenario. Given the information we’ve just studied, it is finally time for the reader to learn Nash equilibrium formally.

Named after economist and mathematician John Forbes Nash Jr., Nash equilibrium is the state/event, where each player holds a certain strategy, such that it is in no single player’s interest to change their strategy into another one, given that all other players remain with their original strategy.

What this means in practice, is that no player will change strategy, as changing won’t better personal payoff. This gives the game a state of balance and stability. It is quite obvious that this isn’t the best possible outcome, but it is the only one where no player is getting at risk.

What made Nash’s concept powerful and relevant to the real world, is that he used maths to prove that in every game, there is a Nash equilibrium. In every situation where we can find payoffs to all outcomes, there is a set of strategies by each player that will be stable.

Though, I am partially lying to you, as the Nash Theorem that proves this existence is a bit more complex. We have only so far seen pure strategies of the Nash equilibrium, but the existence that is implied is that there must either be a pure or a mixed set of strategies that reach a Nash equilibrium.

To understand this, here is a situation that might break our previous strategy:

• You and a friend simultaneously reveal a penny.

• If both pennies show heads or both show tails, your friend has to pay you 1.

• If one penny shows heads and the other shows tails, you have to pay your friend 1.

• This means that when the outcome is equal you gain and when it is different you lose. The payoff matrix for this is:

Heads Tails Heads 1, -1 -1, 1 Tail -1, 1 1, -1

This situation is very common. Take, for example, a game of football. In a penalty kick, you shall either score if you throw the ball to a different side than the side the goalie dived too, but if you both go on the same side, you don't strike a goal.

Now, if you actually go through all values of the table, we know that there is no nash equilibrium.

This is becomes obvious once we analyse all possible events:

• Heads-Heads: in this case, given that both players are playing heads, it is advantageous for the player who loses (your friend) to change to tails, meaning its not a nash equilibrium

• Heads-Tails: in this case, you are losing by keeping heads, meaning you wish to move to tails.

• Tails-Heads: in this case, you are loosing by staying with tails, so you wish to move to heads.

• Tails-Tails: in this case, your friend is losing by staying in tails, so they will move to heads.

Or so we think.

Nash’s Theorem, states that there must be at least one Nash equilibrium for all finite games.

Now how do we account for this theorem? Well, a simply put (oversimplified) answer is that there is another type of Nash equilibrium.

First of all, a finite game is a game that has both a finite number of players and a finite number of strategies for each player.

The type of Nash equilibrium we’ve been dealing with so far is the pure strategy. The other type we shall discus now is the mixed strategy Nash equilibrium. A pure strategy is when a player is 100% of the time only choosing a single action.

Mixed Strategy Nash Equilibrium (MSNE), is described as:

• If no equilibrium exists in pure strategies, one must exist in mixed strategies.

• A mixed strategy is a probability distribution over two or more pure strategies.

First of all, to clarify this dichotomy of pure and mixed strategies, these are concretely defined as “A pure strategy determines all your moves during the game (and should therefore specify your moves for all possible other players' moves). A mixed strategy is a probability distribution over all possible pure strategies (some of which may get zero weight).” So, coming back to MSNE, it is described as:

• If no equilibrium exists in pure strategies, one must exist in mixed strategies.

• A mixed strategy is a probability distribution over two or more pure strategies.

• The players choose randomly among their options in equilibrium.

• If mixtures are mutual best responses, the set of strategies is a mixed strategy Nash equilibrium.

For example, suppose you are playing matching pennies against a mind reader. How can you avoid losing?

In theory, we’d probably think we can’t, since our concrete deterministic pure strategy can be known by the mind reader and therefore combated.

But what if we had a mixed strategy? What if our strategy is to flip the coin? At best, the mind reader could only win half the time.

Now suppose that both players are simply randomly choosing between heads and tails. The payoff matrix for this would be:

Heads (.5) Tails (.5) Heads (.5) 1, -1 -1, 1 Tail (.5) -1, 1 1, -1

Now lets analyse this situation. For player 1, and he is playing heads, he doesn’t really care what choice he makes, because if he chooses heads, half the time he will win, and half the time he will lose, and the same goes for tails.

This therefore puts both tails and heads to be best responses for player 1, given that player 2 is randomly picking heads and tails.

So, coming back to our definition of nash equilibrium: “A Nash equilibrium is a set of strategies, one for each player, such that no player has an incentive to change his or her strategy.”

What have we got in this case? When both players have a ‘flip the coin’ strategy, neither wish to change their strategy, as doing so will not change their outcome.

We’ve got a nash equilibrium!

Current War

Now that we’ve got significant theory laid down, we can start looking at more practical applications of game theory. The one we will focus on today is the Ukraine//Russia war.

To understand the situation as a game theoretic scenario, we shall take the territory at stake (setting of the war), and distribute it according to a ratio of power between both parties. Lets for now place it around the halfway mark of the disputed territory, but remember that this line does not wish to resemble the actual ratio of power between both parties:

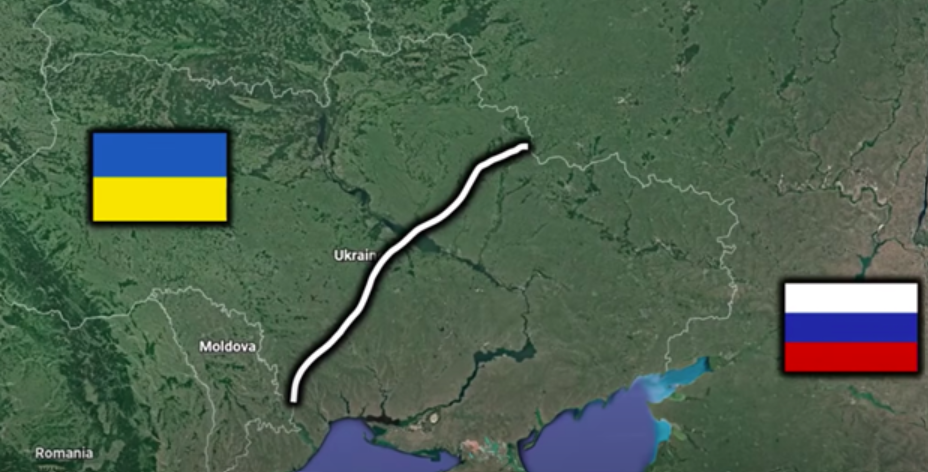
This line is called the settlement line. What this gives us, is a visual intuition of the power distribution between both countries.

Now, since Ukraine only has the power represented by the territory to the left of the line, and Russia only that to the right, each area represents all the power the countries can devote to the war.

We shall now introduce other 2 sections to our map. Lets place lines that signify the active cost of remaining at war of both parties. These will be done so by being between the settlement line and in each countries’s respective territory-representation:

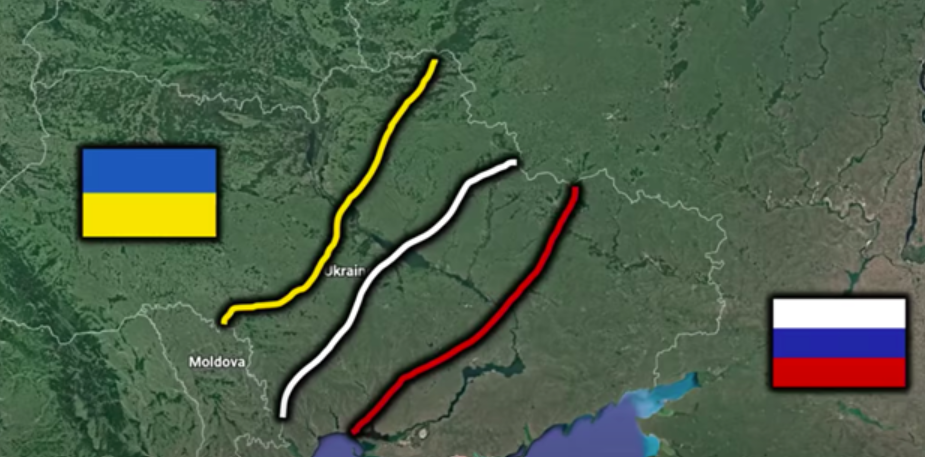
Again, note that these aren’t accurate, but give an idea of the problem at play. What these mean is that in between the yellow and white lines, that area represents the amount of power Ukraine is actively putting into war. Its the cost of war. The same goes for Russia and it’s red line.

Note that a fully fought war is when one side either gives up or loses all resources. What this means either way, is that if either party decides for a fully fought war, they shall resign all their power and territory to the other party.

If the costs for war by Ukraine and Russia are currently those between their lines and the settlement line, any settlement between these 3 lines would be more advantageous than remaining at war, as such will not cost more resources than what both sides are already loosing by even participating in war, meaning that they will save most resources by agreeing upon any new border between the yellow and red lines.

What this also implies is that there is a nash equilibrium for both sides to choose peace given the condition that the current barrier is in between both lines. In that case, it is not in either Russia’s or Ukraine’s interest to keep fighting as they will lose more resources by doing so than by simply staying at peace.

Yet a settlement behind their respective lines wouldn’t be possible as whatever side will lose less resources by continuing to fight rather than making a peace treatment.

Now what would happen if ukraine joined NATO? Ukraine would gain more war power, meaning the settlement line would shift in favour of ukraine.

Therefore, their cost of war would shift along to the right together with the new settlement line. If the new yellow line surpasses the previous red line, it will become clear to both parties that fighting is a significantly better option than remaining at peace, as ukraine will only be satisfied if a settlement is to the right of the yellow line, while russia would only if the settlement would be to the left of the red line:

Now this case leads to a war success for Ukraine, as russia would now have to spend more resources to combat ukraine, pushing Russia’s costs higher until they reach enough to the right for Russia to find advantage in a settlement:

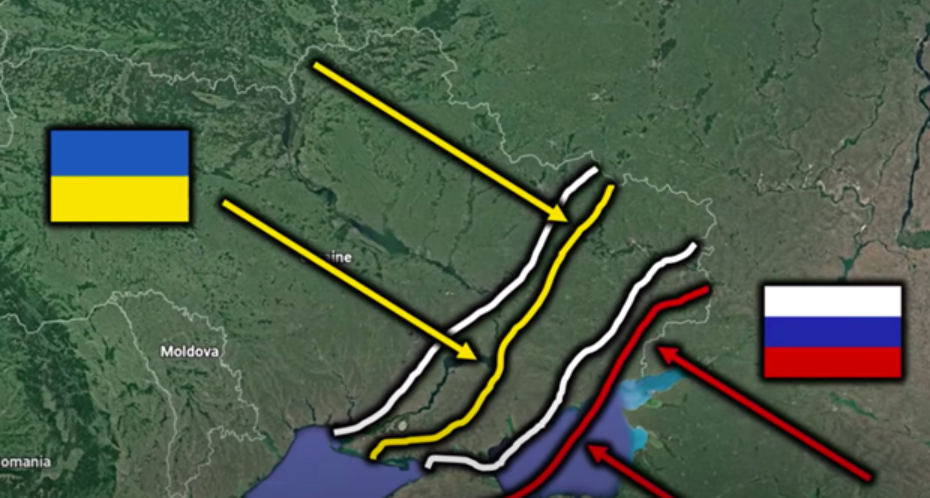
Another case, would be if Russia found a way to get a puppet regime in Ukraine. This would then give Russia a war success, as it would make sure that Ukraine does not join NATO, meaning that Russia could then safely put more resources into the war without risking as much, as Ukraine wouldn’t have a chance to get help from NATO.

History

John von Neumann is considered one of the founding fathers of Game Theory and Economical Behaviour Analysis. This is largely due to his work “Theory of Games and Economic Behavior”. In it, he took existing and made new economical concepts that predict behaviour while doing so in a mathematical language which is now the game theoretic language.

While the first John in this story made significant contributions, the most essential John to game theory is John Forbes Nash Jr. Nash made Nash equilibrium, which (as this article shows) is a foundational step in solving games. While the current view of the Nash equilibrium you have involves words, John Nash made the equilibrium in a fully mathematical language, and proved the existence of such an equilibrium in all games in his debut paper "Equilibrium Points in N-person Games" which was also his first published and his PhD thesis.

Even though Nash’s equilibrium is still in wide use and makes mathematical sense, there are improvements to it that have been made over time. The most notorious include Trembling Hand Perfect equilibrium developed by Reinhard Selten, Correlated equilibrium by Robert Aumann, and Proper equilibrium due to Roger B. Myerson which developed further on Selten’s work.

The field of game theory doesn’t fully revolve around the equilibrium used, as it is applied into other areas of maths, science, and humanities.

Applications include, the “Common Knowledge” game theory, which combines information theory with game theory, creating for a more general game playground where different players may have different information that influences their payoffs, Evolutionary game theory, which applies game theory into darwinian evolution contexts, and Design Game theory, largely developed by Leonid Hurwicz, Eric Maskin, and Roger Myerson, which is now used as a tool for governmental agencies and other policy makers to design rules that will be effective.

Epilogue

As mentioned earlier, game theory has large influences from the works of John Nash. His contributions made such significant impacts that he is now known in the mainstream, partially due to the 2001 biographical movie “A Beautiful Mind”, that contains a chronological story of Nash’s life and speculation and purposeful distortion on his actual life story (likely for entertainment reasons).

I would like to end this article on a more direct address style. Game theory can be used in your own life, not necessarily by means of rigorous mathematical thinking, but more accessibly by logical reasoning and an understanding of the concepts of game theory. The game theorist mindset allows one to ponder at a situation by treating each involved individual as a player, who wishes to achieve and act in different ways in order to maximise their payoffs. I know this is not very practical advice, but from personal experience, once you view things from a perspective of cause and effect, reward and punishment, I was able to find and make better decisions.