CNNs, pooling and filtering: image recognition in neural networks

Abstract

To begin, I would like to explain that in the study of neural networks, there are 3 different but powerful perspectives: the mathematician’s, computer scientist’s and psychologist’s. All 3 are distinct yet explain the reasoning of neural network behaviour in beautiful ways. I will aim to provide all 3 perspectives, as this will further enrich the reader’s understanding of neural networks, and try to answer the question: how could someone have invented such a thing.

Background knowledge

The knowledge for the understanding of the key concepts in image recognition AI is pretty simple, it is only needed a basic understanding of neural networks, more specifically,

That neural networks are made up of pattern recognizing nodes/neurons, that through statistical learning methods, fit the pattern such that they activate when a pattern is shown to be present, thus the neural network combines these various pattern detecting neurons to output accurate results. (computer scientist perspective)

Convolution

Say that by using a CNN, we would want a neural network to distinguish an X from a 2d image as a (1,0) output, and an O as a (0, 1) output. This means that the nodes that form up to the first node of the last layer should all identify X image patterns, while the ones leading up to the second node of the last layer would identify O image patterns. For this to happen, we would want our Net to have distinct nodes that don’t overlap too much leading to the last two nodes, such as abstract features each on their own.

To do so, let's say we tried to collect exact parts of images to be considered when computing the next node’s output, this would mean that some nodes would not connect in between layers. What makes this tricky, is that not all images are the same:

What a computer sees is:

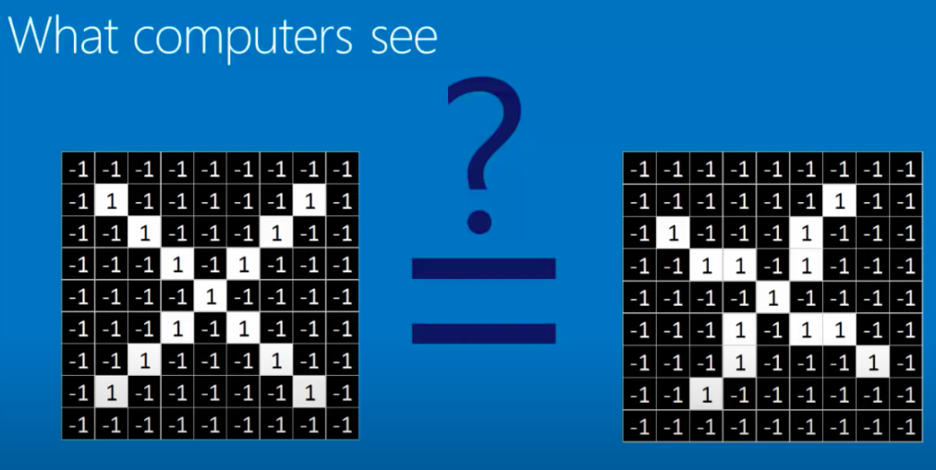
Which makes it hard, especially when it comes to flattened data. Conv nets solve this by performing the convolute operation on convolution layers, where it filters a larger images into blocks, meaning that different nodes would not be fully connected to the last layers, resulting in easier pattern recognition:

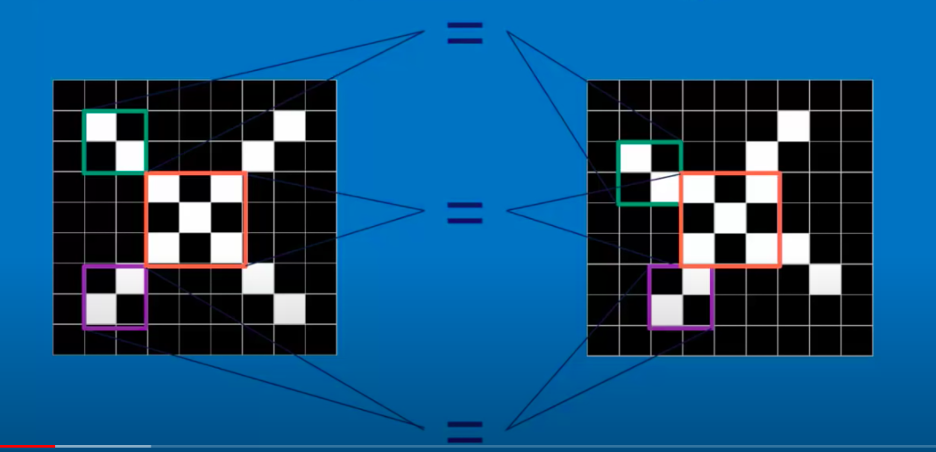
These filters would then have to notice patterns by activating on the similarity in their points with the other inputted points:

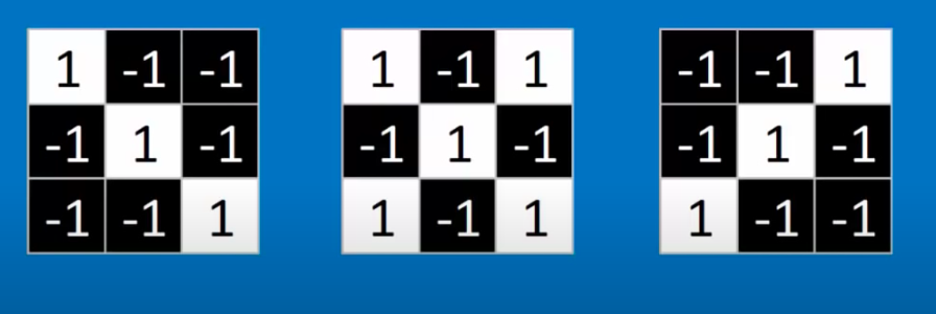
Now as we know, the operation that finds the similarities between two number groups is the dot product, thus, by taking the dot product of the filters and the different blocks of the images, the similarities would be found and the pattern would be learned, and as a matter of formatting, the dot product result would then be divided by the size of the pixels, simply to avoid many pixels resulting in large results.

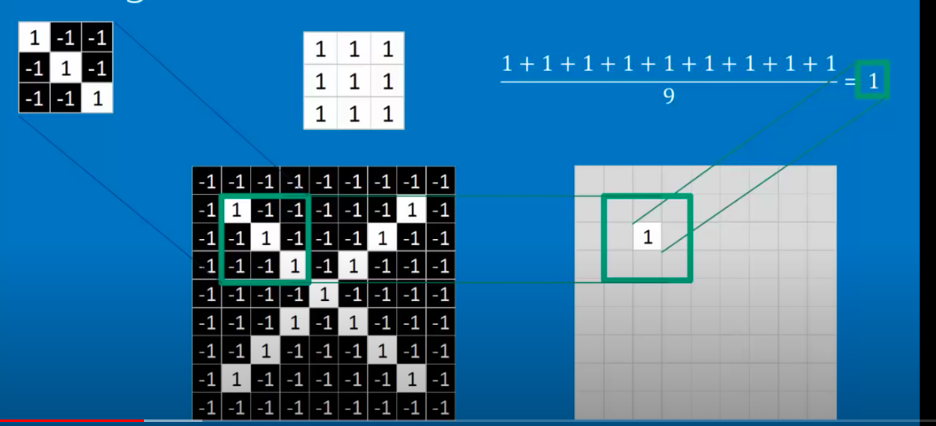
In this case, we would get our neuron output 1. We then would move the filter around the image to find how much the filter matches up in every other place of the image.

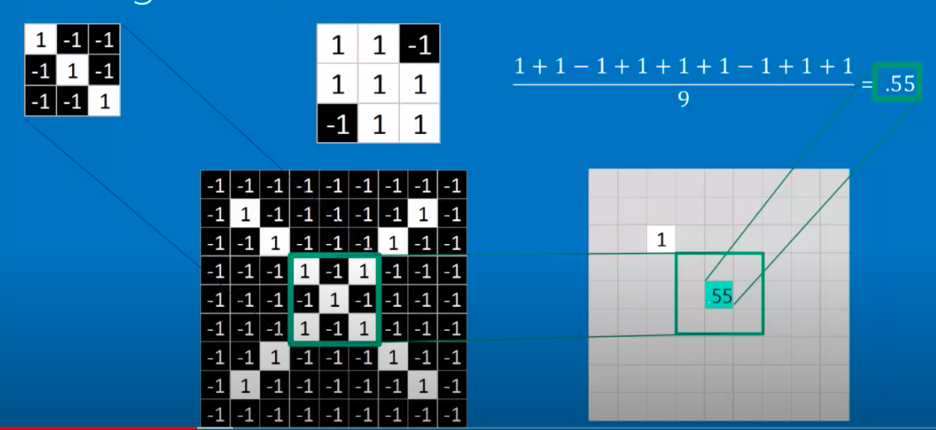
Thus, convolution is the repeated application of this filter:

We can thus apply this with many filters:

Pooling

Pooling is an operation for reducing the dimensionality of a 2d array while preserving its information. It works on two features: filter and stride. Filter is the size of the block being chosen, and stride is how much this filter moves each time:

In the case of max pooling, the filter will take the maximum value, and in average pooling, the average value.

As we can see in the image above, pooling does a fairly good job at keeping the pattern found.

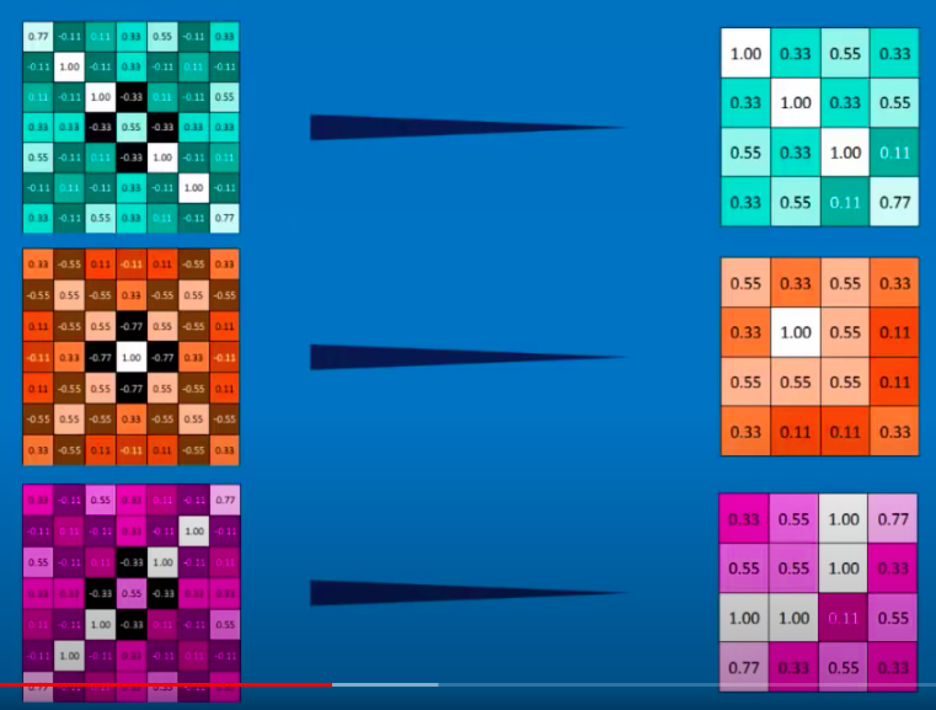
the key thing about pooling is that a stack of images becomes a smaller stack of images (while keeping the pattern).

We might then apply the standard reule to change negatives to zero. Then, we stack these layers:

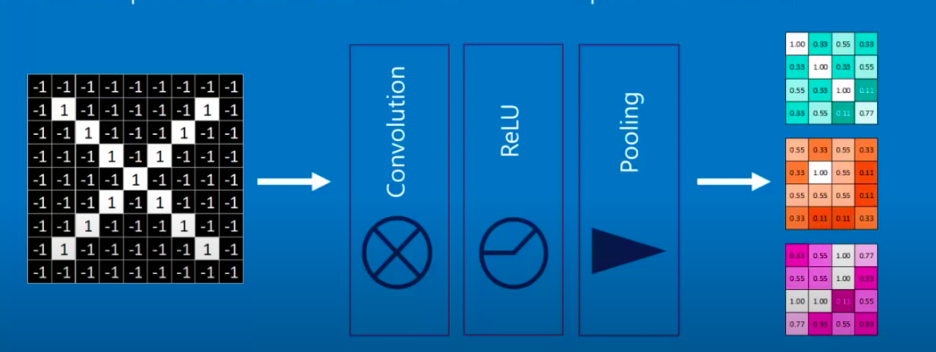
And after several tries, we get the right output.

Recap

To conclude, the key parameters of convolution are the number of features and the size of features, for pooling, they are the window size and stride, and for a fully connected layer it's the number of neurons. The process of CNNs is only good for spatial data that have some sense of 2dness or 3dness, and it won't be useful for other types of data.

Gabriel Gramicelli Y9